Recent Projects
Professional Experience
Awards and Scholarships
Lectures and Conference Presentations
Publications
Courses and Workshops
Exhibitions
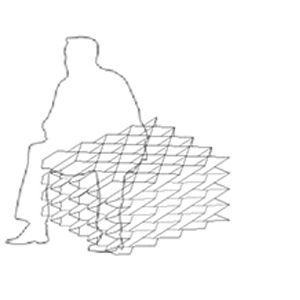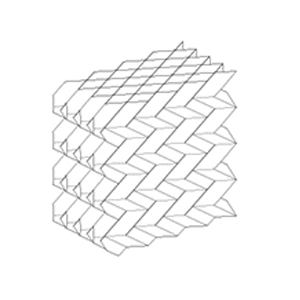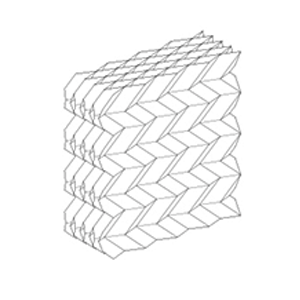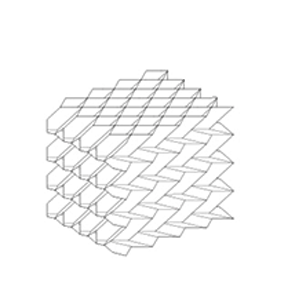
Minimum Spanning Tree vs. Maximum Spanning Tree
How to create efficient unrolling segmentation for hemisphere?Spring 2024
@Generative systems for design, 62-706, Carnegie Mellon University
Implementation tool: Grasshopper, Rhino3D
Instructor: Jingyang (Leo) Liu
Collaboration: Sherry Yujin Wu
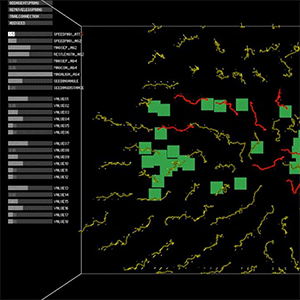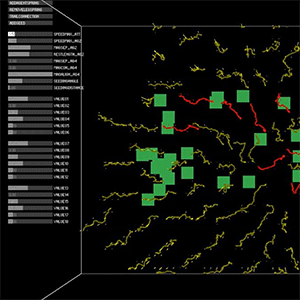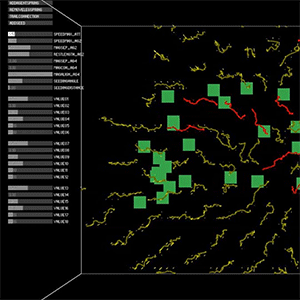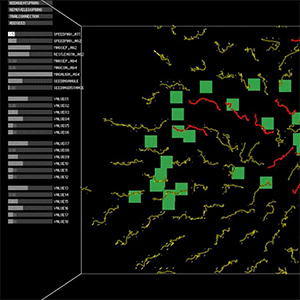
We planned to test two folding methods using IVY plug-in in Grasshopper which has Minimum Spanning Tree component.
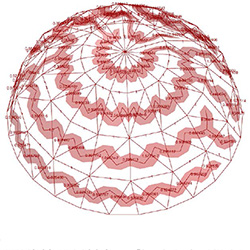
Often, running a minimum spanning tree algorithm on the weighted mesh graph helps optimize for various global properties. One criterion often considered is the dihedral angle, which denotes the angle between two connecting faces. However, it’s unclear to the team how minimizing the dihedral angle actually impacts the assembly experience. To investigate further, we designed a special hemisphere and unrolled its meshes by employing both maximum and minimum spanning tree algorithms. These unrolled meshes were then printed on a suitable material and assembled, aiming to gain insights into the practical effects of minimizing the dihedral angle.
Finding the facet angle difference using Polygon meshing parameters
Maximum angle is 50 degree(left) 30 degree(right) respectively
Mesh study, finding the tendency
While generating polygon mesh based on hemisphere shape, we tested the base shape with Rhino’s polygon meshing parameter. We observed that vertical facet angles are usually bigger than horizontal facet angles. The images left show this tendency.
Definition of Dihedral angle
![]()
Segmentation of hemisphere
![]()
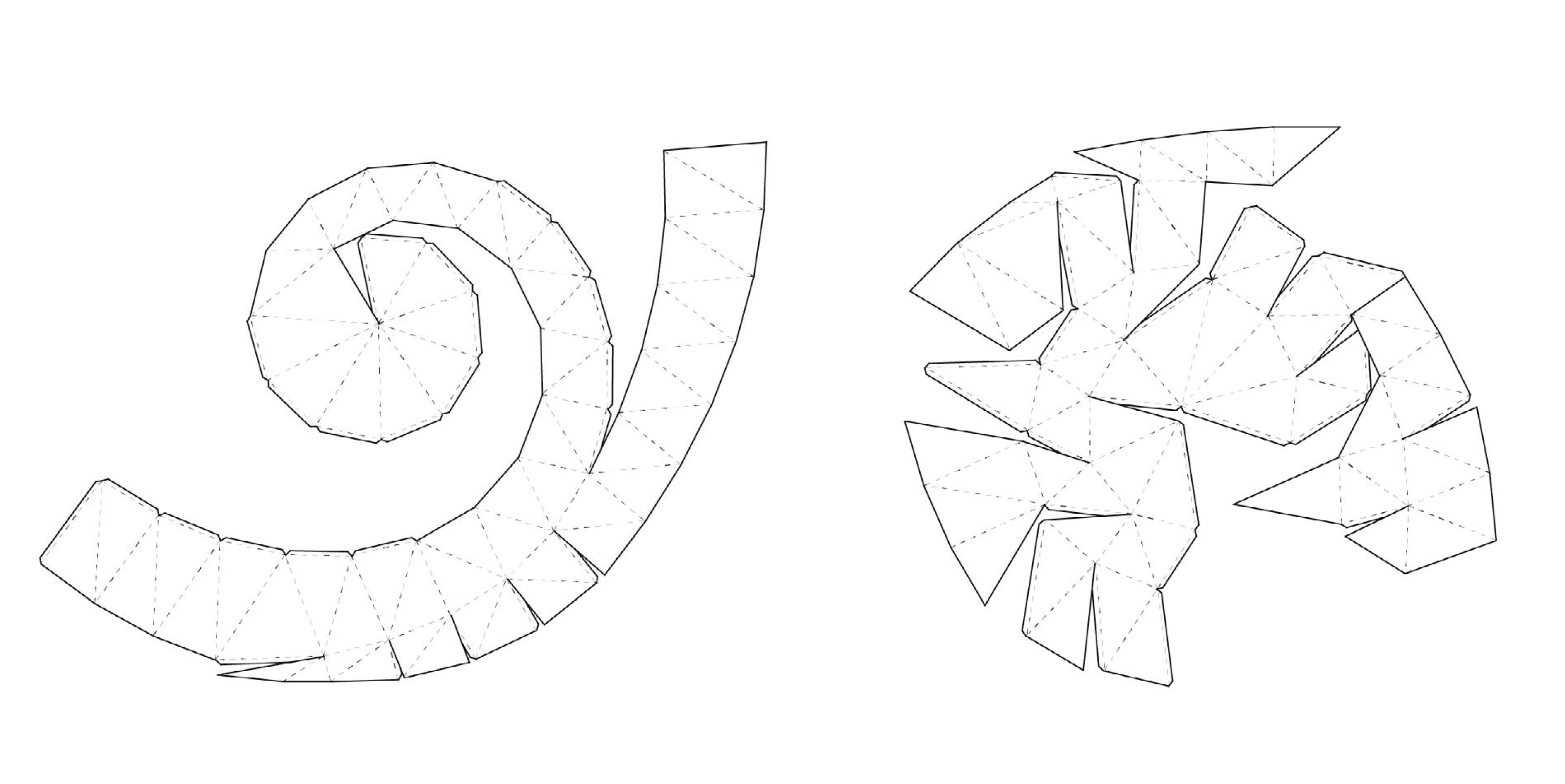
Same angle division in the vertical section. (Left)
The actual spiral shape consisting of facets with small angular difference. (Right)
Segmentation of hemisphere
Same angle division in the vertical section. (Left)
The actual spiral shape consisting of facets with small angular difference. (Right)
Define Dihedral angle
During tests, we have to redefine the meaning of Dihedral angle, because according to the face direction or type of components, ‘edge angle’ is interpreted differently. Although dihedral angle defined in the class was the inner edge angle of polygon mesh, we followed the edge angle we used in Rhino’s polygon meshing parameter to lessen the confusion.
Maximum spanning tree
Minimum spanning tree
Maximum spanning tree in hemisphere
Minimum spanning tree in hemisphere
Results of development diagram using spanning tree
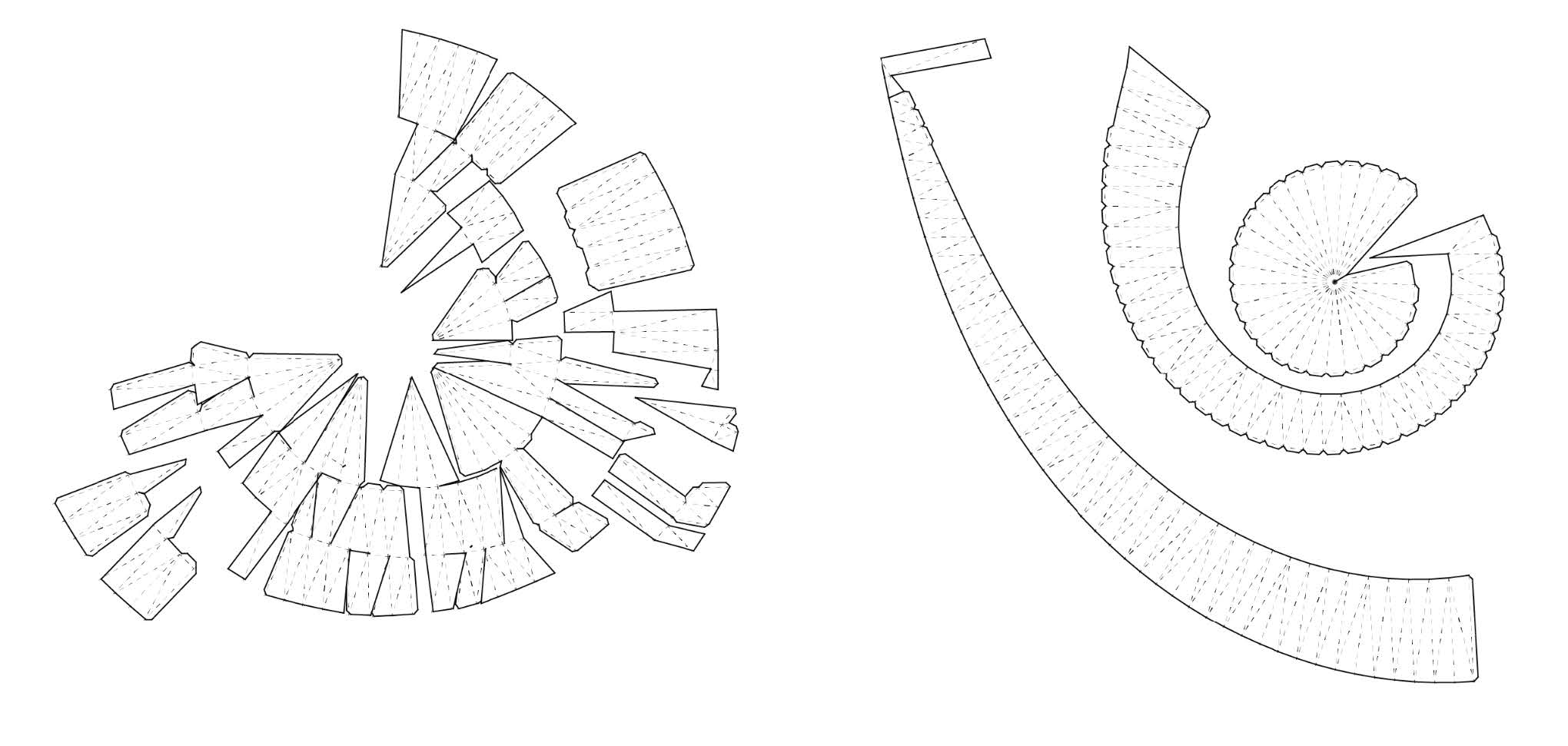
Design a spiral Hemisphere applying Minimum Spanning Tree vs Maximum Spanning Tree
To make a dramatic comparison between the two developments, we devised a spiral mesh consisting of facet angles in which the edge-angle of each facet is aligned almost unfolded horizontally and almost equally vertically.
Fabrication
In our experiment, both hemispheres constructed using the minimum spanning tree and the maximum spanning tree were crafted from paper. Craft paper possesses sufficient strength to form a self-supporting structure while being easier to fold due to being half-cut, compared to materials like chipboard or acrylic. After unrolling the mesh in Rhino, we utilized Autocad to create a .dxf file for laser cutting.
Overall, we found the hemisphere created from the minimum spanning tree simpler to assemble.
Two main reasons support this observation:
01. The flaps (sections requiring glue) in the hemisphere created from the minimum spanning tree were longer and more continuous. This facilitated the gluing process as it as easier to fold and apply glue along these lines by a single person.
02. Additionally, the laser cuts along the fold lines were not deep enough, resulting in only surface scratches. Consequently, many folds were not sufficiently pronounced, impacting the assembly process.
Conversely, the hemisphere constructed from the maximum spanning tree had numerous neighboring faces with larger dihedral angles.
This necessitated more force to hold the glued parts together, increasing the likelihood of breakage during assembly. We have used the ThinMesh function in the grasshopper to print out the MeshGraph for better visualization.
Reflection
In the method Minimum Spanning Tree, we recognize that facets with smaller (nearly unfolded) angle differences are more likely to fold without using split flaps, as their flap assembly is prone to weaknesses. Facets with greater edge angles can support themselves more effectively, even when assembled with split flaps.
In our case, we have done some reverse engineering. We had the idea of spiral unfolded shape first, then we tried to design how we should mesh the hemisphere. It will be helpful to test both unfolding techniques on a greater variety of 3D shapes.
On a second read of the Ivy manual, we have also realized that Orange Peel Edge could be a tool to achieve a similar result of the spiral shaped resulted from the maximum spanning tree.
